Disjoint Sparse Table とセグ木に関するポエム

2018/09/09 実装を少し変更しました

2021/02/18 数式を tex を使ったものに変更しました

2021/02/18 不適切な表現を変更しました

2021/02/18 msb の意味が適切でなかったので、修正しました

前半:

https://discuss.codechef.com/questions/117696/tutorial-disjoint-sparse-table

これの日本語解説

後半:

ポエム

Disjoint Sparse Table とは

　Disjoint Sparse Table は静的な半群列の区間和を高速に計算できるデータ構造です。具体的には要素列長を $N$ としたとき、構築 $\mathrm { O } ( N \log ( N ) )$ /クエリ $\mathrm{O}(1)$ を達成します。半群は演算が閉じていて結合則を満たせばいいので該当するものは多く、単純な和や積、 $\mathrm{xor}$ 、 $\min$ 、 $\gcd$ などが該当します。

※都合のため、クエリは閉区間で表現します。

お気持ち

　基本的には累積和の考え方を使います。まず、中央から左右の方向に累積和を取ることを考えてみます。(下図参照)

f:id:noshi91:20180508173637p:plain

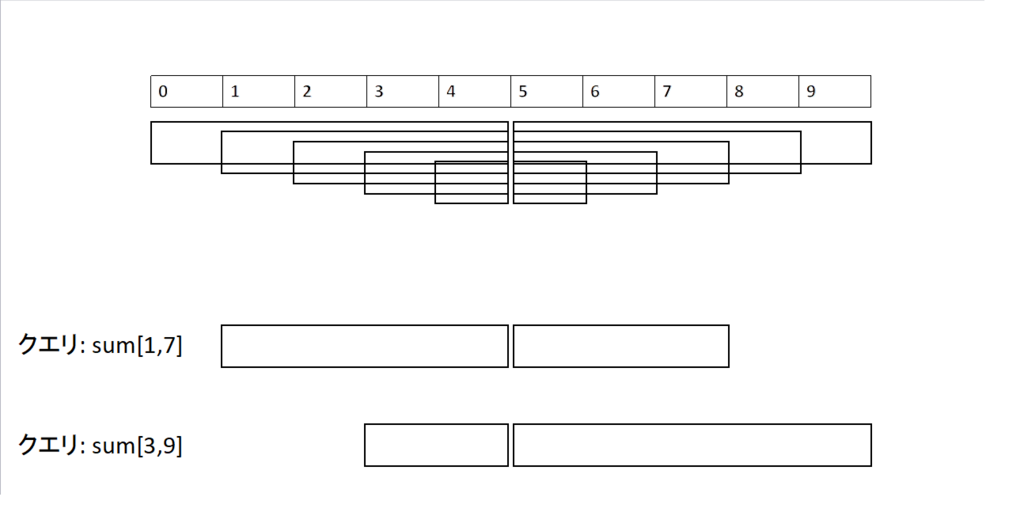
それぞれのクエリに対して、右と左から対応する累積和を出してきて足します。こうすると、中央の境目を跨いでいる区間クエリについては $\mathrm{O}(1)$ 時間で計算できることが分かります。

データの持ち方と構築

　問題は境目を跨いでいないクエリが計算できないことです。そこでこの「中央を跨ぐクエリを計算できる構造」をセグ木と同じ形状に乗せてみることにします。(下図参照)

f:id:noshi91:20180508175130p:plain

見づらいかもしれませんが、セグ木のノードに対応する区間の累積和を乗せています。クエリ $\lbrack 9,13 \rbrack$ の例を見てください。 $7$ - $8$ の境界を跨いでいないため一番上の段では処理が出来ませんが、 $11$ - $12$ を跨いでいるため上から $2$ 段目右の部分で処理が可能です。他のクエリの例も試してみて欲しいのですが、必ず何れかの段で計算可能であることが分かると思います。この構造は二次元配列に素直に累積和を取って行けばよいため $\mathrm{O}(N \log (N) )$ で構築が可能です。

クエリ

　次に問題となるのはクエリの時に、どの段を使用すればいいかを高速に判定する部分です。上の段から境界を跨いでいるかチェックしていては $\mathrm{O}(\log (N) )$ 時間掛かってしまうことが分かると思います。そこでbit演算を使います。具体的には閉区間で与えられたクエリの右端、左端のインデックスの $\mathrm{xor}$ を取り、その最も左の $1$ の位置 (most significant set bit) を計算します。

クエリ $\lbrack 9,13 \rbrack$ を例にすると, $1001 \mathop{\mathrm{xor}} 1101 = 0100$ となります。一番左の $1$ が使用すべき段を示しています。この場合は左から $2$ 番目なので使用するのは上から $2$ 段目になります。

クエリ $\lbrack 5,12 \rbrack$ ではどうでしょうか。 $0101 \mathop{\mathrm{xor}} 1100 = 1001$ となり一番左の $1$ は左から $1$ 番目にあります。よって使用するのは上から $1$ 段目＝最上段になります。

これはそれぞれの境界を跨ぐときに対応する桁がインクリメントされることから分かります。例えば $3$ - $4$ の境界を通ると $4$ の位が $0$ から $1$ になるため $\mathrm{xor}$ を取ったときに $1$ になります。

　これで使用すべき段を $\mathrm{O}(1)$ 時間で判定し、 $\mathrm{O}(1)$ 時間でのクエリ処理が可能になりました。嬉しい。

ポエム(読み飛ばし推奨)

　半群というと近い構造にモノイドがあります。モノイドと言えばセグ木ですが、セグ木は半群でも扱うことができます。ここで時々聞く話として「セグ木は半群でもOKなら、半群を扱えるデータ構造として認識するべきではないか(そのほうが前提条件が緩くなるため)」という問題提起があります。

　しかし私はセグ木は飽くまでも「モノイドを扱うデータ構造」であると主張したいです。これは書いたことがある人ならばわかると思うのですが、非再帰セグ木はモノイドでないとコードがとても冗長になります。単位元を仮定しないことによって場合分けが増えるのですが、この場合分けというのは半群にbool値を付けてモノイドに拡張しているのと本質的にはなんら変わらないのです。一方で Disjoint Sparse Table は単位元を仮定しなくても場合分けは増えません。ですから、半群は必ずモノイドに拡張できる*1ことも合わせてセグ木はモノイドを扱うとした方が美しいと思うのです。

2023/12/12: やっぱそうでもないかもしれない Disjoint Sparse Table に乗るのはやはりモノイドかもしれない。 - noshi91のメモ