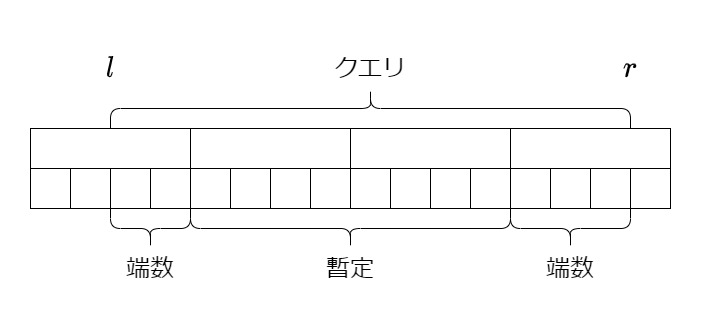
概要
Convex Hull Trick で最小値取得クエリの が整数の時、アルゴリズム内で直線が不要かどうかチェックする部分を簡単に記述することが出来る。
特に、傾きと切片を掛けることでオーバーフローする問題を発生させない。
本文
Convex Hull Trick で、最小値取得クエリの の値の全てが整数とします。
簡単な下処理により、直線の傾きは distinct と仮定してよいです。
本の直線
があり、
とします。
ここで、
が不要かどうか判定することを考えます。
本の直線が下図のような位置関係にあるとしましょう。
座標軸の目盛りは整数の座標を表しています。
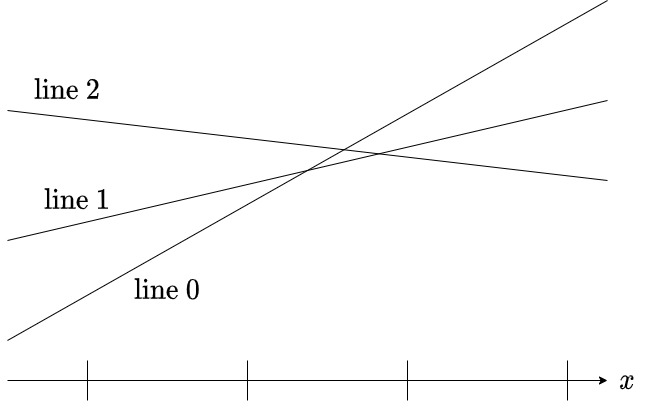
Convex Hull の字面に従うならば、 は最小値を取り得る、すなわち必要な直線です。
しかし、クエリが整数しかないという仮定の下、
は最小値を取り得ません。
この条件を正確に記述します。
\begin{align} f(ax+b, cx+d) := \max \lbrace k \ | \ ak+b \leq ck+d \rbrace \end{align}
と定義すれば、
\begin{align} \text{line}\ 1 \text{が最小値を取り得る} \Leftrightarrow f(\text{line}\ 0, \text{line}\ 1) < f(\text{line}\ 1, \text{line}\ 2) \end{align}
です。
ただし、 直線が交わる
座標では傾きの大きい方が最小値を取るとしています。
ところで の仮定の下
\begin{align} f(ax+b, cx+d) :&= \max \lbrace k \ | \ ak+b \leq ck+d \rbrace \\ &= \left \lfloor \frac {d - b} {a - c} \right \rfloor \end{align}
であるため、 は整数除算で計算することが出来ます。
これにより、分母を払って判定するアルゴリズムにおけるオーバーフローの問題が発生しなくなります。
また、この条件はクエリが実数の場合の条件より強い条件なので、残された直線群の 凸 性が保たれ、最小値取得クエリのアルゴリズムは普通の物を使うことが出来ます。