2023-05-10

多項式の基底変換　メモ

Bostan, A., & Schost, É. (2005). Polynomial evaluation and interpolation on special sets of points. Journal of Complexity, 21(4), 420-446. の内容と、FFT で計算したときの計算量のメモ

2023/12/13: 計算量の定数倍を一部訂正(改善)しました

Question	General	Arithmetic	Geometric
Newton → Monomial	自然な分割統治	General と同じ	q-二項定理で展開すると q-exp
Monomial → Newton	noshi91のメモ	General と同じ	q-exp の逆元
Monomial evaluation	hly1204's blog	General と同じ。Newton 基底経由でも可	ア辞典
Monomial interpolation	ei1333の日記	微分の多点評価を $\mathrm{O}(n)$ で計算できる。Newton 基底経由でも可	ア辞典, Newton 基底経由でも可
Newton evaluation	Monomial 基底を経由	式変形すると exp	式変形すると q-exp
Newton interpolation	Monomial 基底を経由	exp の逆元	q-exp の逆元

支配的でない項は書かない。
長さ $n ~ (2$ 冪 $)$ の DFT が $n \log _ 2 (n) = n \operatorname{lb} (n)$ で計算できるとする。
$\mathrm{O}(n \operatorname{lb}(n) )$ になっている部分は、 $n$ が $2$ 冪だとして定数倍を評価している
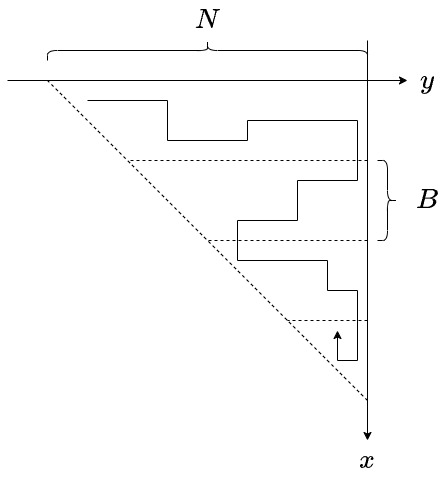
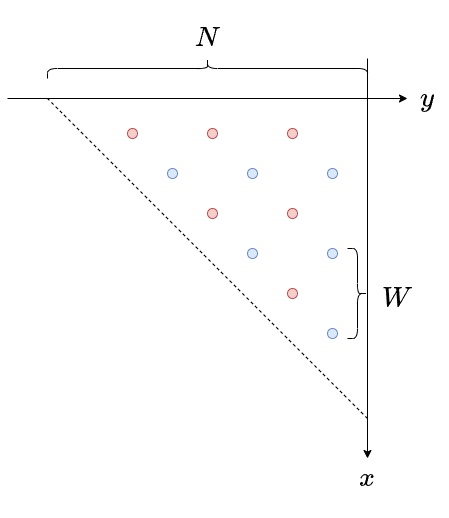
subproduct tree の計算は $n \operatorname{lb}(n) ^ 2$

Question	General	Arithmetic	Geometric
Newton → Monomial	$2 ~ n \operatorname{lb}(n) ^ 2$	$2 ~ n \operatorname{lb}(n) ^ 2$	$6 ~ n \operatorname{lb}(n)$
Monomial → Newton	$2 ~ n \operatorname{lb}(n) ^ 2$	$2 ~ n \operatorname{lb}(n) ^ 2$	$6 ~ n \operatorname{lb}(n)$
Monomial evaluation	$2 ~ n \operatorname{lb}(n) ^ 2$	$2 ~ n \operatorname{lb}(n) ^ 2$	$6 ~ n \operatorname{lb}(n)$
Monomial interpolation	$3 ~ n \operatorname{lb}(n) ^ 2$	$2 ~ n \operatorname{lb}(n) ^ 2$	$12 ~ n \operatorname{lb}(n)$
Newton evaluation	$3 ~ n \operatorname{lb}(n) ^ 2$	$6 ~ n \operatorname{lb}(n)$	$6 ~ n \operatorname{lb}(n)$
Newton interpolation	$4 ~ n \operatorname{lb}(n) ^ 2$	$6 ~ n \operatorname{lb}(n)$	$6 ~ n \operatorname{lb}(n)$

2023-05-01

転置原理なしで Monomial 基底から Newton 基底への変換

概要

[1] において解説されている、Newton 基底から Monomial 基底への変換のアルゴリズムを、転置原理無しで説明する。問題は以下の通り。

体 $\mathbb{K}$ 上の $n$ 次未満の多項式 $\displaystyle f(x) = \sum _ {i = 0} ^ {n - 1} c _ i x ^ i$ と、 $n$ 個の値 $p _ 0, p _ 1, \dots, p _ {n - 1}$ が与えられる。 $\displaystyle f(x) = \sum _ {j = 0} ^ {n - 1} d _ j \prod _ {k = 0} ^ {j - 1} (x - p _ k)$ を満たす $d _ 0, d _ 1, \dots, d _ {n - 1}$ を求めよ *1。

これを $\Theta(n (\log(n) ) ^ 2 )$ の時間計算量で解く *2。

$\mathbb{K} ( ( x ^ {- 1} ) )$ と多項式の余り付き除算

$\mathbb{K} ( ( x ^ {- 1} ) )$ は、有限の整数 $n$ と $c _ i \in \mathbb{K}$ に対して $\displaystyle \sum _ {i = - \infty} ^ {n} c _ i x ^ i$ と表されるような形式的な和に対し、自然に和や積を定義することで得られる体である。定義より、 $\mathbb{K}$ 上の多項式は全て $\mathbb{K} ( ( x ^ {- 1} ) )$ に含まれる。 $\mathbb{K} ( ( x ^ {- 1} ) )$ は多項式の余り付き除算と関係していることを説明する。

$f(x), g(x)$ をそれぞれ多項式で $g(x)$ は $0$ でないとする。 $f(x)$ を $g(x)$ で余り付き除算することを考えると、以下のような式を得る。

\begin{align} f(x) &= q(x) g(x) + r(x) \end{align}

ここで $q(x), r(x)$ は多項式であり、 $r(x)$ の次数は $g(x)$ の次数未満である。この式を $\mathbb{K} ( ( x ^ {- 1} ) )$ 上で考えて両辺を $g(x)$ で割ると

\begin{align} \frac{f(x)}{g(x)} &= q(x) + \frac{r(x)}{g(x)} \end{align}

となる。 $g(x)$ の次数を $d$ とすると、 $\frac{1}{g(x)}$ は $x ^ {- d}$ 以下の次数の項しか持たない *3。すると $r(x)$ の次数と併せて、 $\frac{r(x)}{g(x)}$ は $0$ 次未満の項しか持たないことが分かる。一方で $q(x)$ は多項式だから $0$ 次以上の項しか持たず、 $\frac{f(x)}{g(x)}$ の $0$ 次以上, 未満の項と $q(x), \frac{r(x)}{g(x)}$ が完全に対応していることが分かる。 $f(x)$ を $g(x)$ で割った余り $r(x)$ を計算したいときは、 $\frac{f(x)}{g(x)}$ の $0$ 次未満の項を取り出して $g(x)$ を掛ければよいということになる。実際には $-d$ 次から $-1$ 次までの項を計算して、 $g(x)$ を掛けた後 $0$ 次以上の項を取り出せばいい。

転置原理と多項式乗算が絡んだアルゴリズムは、自然な解法を多項式の余り付き除算で書き表して、 $\mathbb{K} ( ( x ^ {- 1} ) )$ を用いて式変形すると等価なものが導出できることがそこそこある。

Monomial 基底から Newton 基底への変換

求めるのは、以下の式を満たす $d _ i$ であった。

\begin{align} f(x) &= \sum _ {j = 0} ^ {n - 1} d _ j \prod _ {k = 0} ^ {j - 1} (x - p _ k) \end{align}

$0 \leq t \lt n$ を満たす整数 $t$ について、両辺を $\displaystyle T _ {t} (x) := \prod _ {k = 0} ^ {t} (x - p _ k)$ で割った余りを取ると

\begin{align} f(x) \bmod T _ t (x) &= \sum _ {j = 0} ^ {t} d _ j \prod _ {k = 0} ^ {j - 1} (x - p _ k) \end{align}

を得る。さらに両辺の $t$ 次の係数を見ると、

\begin{align} \lbrack x ^ {t} \rbrack \left( f(x) \bmod T _ t (x) \right) &= d _ t \end{align}

を得る。前述した議論より、この式の左辺は $\mathbb{K} ( ( x ^ {- 1} ) )$ 上で $f(x) / T _ t (x)$ を計算し、その $0$ 次未満の項のみを取り出して $T _ t (x)$ を掛け、 $t$ 次の係数を取り出すことで計算できる。ここで $T _ t (x)$ が $t + 1$ 次の多項式であることに着目すると、結果の $t$ 次の項に寄与するのは、 $f(x) / T _ t (x)$ の $- 1$ 次の項と $T _ t(x)$ の $t + 1$ 次の項との積だけである。さらに $T _ t (x)$ は monic だから、結局以下の式を得る。

\begin{align} \lbrack x ^ {- 1} \rbrack \frac{f(x)}{T _ t(x)} = \lbrack x ^ {- 1} \rbrack \frac{f(x)}{\prod _ {k = 0} ^ {t} (x - p _ k)} = d _ t \end{align}

$\displaystyle \frac{f(x)}{\prod _ {k = 0} ^ {t} (x - p _ k)}$ を、 $\displaystyle \frac{f(x)}{\prod _ {k = 0} ^ {n - 1} (x - p _ k)}$ に $\prod _ {k = t + 1} ^ {n - 1} (x - p _ k)$ を掛けることで計算すると考える。これを全ての $t$ に対して計算するには、多点評価のアルゴリズムの分割統治のような具合で分割統治を行えばよい。最終的な答えに影響する部分の係数だけを管理すれば、時間計算量は $\Theta(n (\log(n) ) ^ 2 )$ となる。

参考文献

[1] Bostan, A., & Schost, É. (2005). Polynomial evaluation and interpolation on special sets of points. Journal of Complexity, 21(4), 420-446.

*1: $p _ {n - 1}$ が使われていないのだが、定義しておいた方が少し都合がよい

*2:畳み込みが $\Theta(n \log(n) )$ 、四則演算が $\Theta(1)$ と仮定している

*3:逆元の定義を考えよ

2023-04-13

定数倍が最適な Mo's Algorithm

アルゴリズム

概要

端の移動回数が $N \sqrt{Q} + \mathrm{O}(N)$ 以下の Mo's Algorithm を思いついたので紹介する。

通常の Mo's Algorithm

Mo's Algorithm の問題設定は以下のように言い換えられる。

$0 \leq x \leq y \leq N$ を満たす格子点 $(x, y)$ が $Q$ 個与えられる。 $(0, 0)$ から始めて全ての点を通る経路を構成せよ。経路の長さはマンハッタン距離で測られ、短いほど良い。

スタートが $(0, 0)$ だけではなく任意の $x$ に対する $(x, x)$ であるとか、色々と実用に即したバリエーションは考えられるが、基本的に $\mathrm{O}(N)$ の変化しかないと思う。

通常の Mo's Algorithm は以下のように経路を構成する。

つまり、 $x$ を幅 $B$ 毎に分け、同じ分類の点を $y$ の順に廻る。また、 $y$ の昇降は交互に変化させる。このとき経路長は $\displaystyle \frac{N ^ 2}{2 B} + QB + \mathrm{O}(N)$ 以下となり、 $\displaystyle B = \frac{N}{\sqrt{2Q} }$ とすれば $\sqrt{2} N \sqrt{Q} + \mathrm{O}(N)$ 以下となる。

改善された Mo's Algorithm

$x$ を幅 $B$ で分けた領域を帯と呼ぶことにする。 Mo's Algorithm の最悪ケースは、点が帯の両端に分布している場合である。しかしこの場合、隣り合う帯の端にある点をまとめて通ってしまえばむしろ普通より短くなることが分かる。この発想で、全ての帯を $B / 2$ だけずらした Mo's Algorithm を実行し、元のものとのうち短い方の経路を選ぶというアルゴリズムを考える。

このアルゴリズムの価値は、 $x$ 座標の変化量を $QB$ より精密に評価することで明らかになる。 $l \leq x \lt l + B$ の帯について、 $\displaystyle x = l + B / 2$ を帯の中央と呼ぶことにする。経路を「中央を通って次に訪れたい点と $y$ 座標を揃えたのち、 $x$ 座標を揃え、再び中央に戻る」ものとして解析しても問題ない *1。すると、各点 $(x _ i, y _ i)$ の $x$ 座標に関する経路長への寄与は、属する帯の中央を $x = c$ として $2 \lvert x _ i - c \rvert$ と評価できる。 $\lvert x _ i - c \rvert$ は最悪で $B / 2$ になり得るが、 $2$ 通りの経路におけるそれを合計すると、常に $B / 2$ になることが分かる (！)。よって $2$ 通りの経路の長さの和は $\displaystyle \frac{N ^ 2}{B} + QB + \mathrm{O}(N)$ であり、 $\displaystyle B = \frac{N}{\sqrt{Q}}$ とすれば $2 N \sqrt{Q} + \mathrm{O}(N)$ で抑えられる。このうち短い方は $N \sqrt{Q} + \mathrm{O}(N)$ 以下である。

最適性

このように点を配置する。赤い点は $1$ 辺に $\sqrt{Q}$ 個配置しており合計で $Q / 2$ 個、青い点と併せて $Q$ 個となる。どの $2$ 点も $W = N / \sqrt{Q}$ のマンハッタン距離があることが分かるから、どのような経路も $Q W = N \sqrt{Q}$ の長さが必要となる。実際には $\sqrt{Q}$ が整数とは限らないこと、格子点にしか点を置けないこと、を考えると $N \sqrt{Q} + \mathrm{O}(N + Q)$ の下限を得る。よって、前述したアルゴリズムは $\mathrm{O}(N + Q)$ の差を除いて最適である *2。

Rollback Mo

参考: https://snuke.hatenablog.com/entry/2016/07/01/000000

同様の考え方を使うと、Rollback Mo も $N \sqrt{Q} + \mathrm{O}(N)$ (Rollback も含めるとこの $2$ 倍) になる。ただしこちらは最適なのか分からない。必ず $\displaystyle \sqrt{\frac{2}{3}} N \sqrt{Q}$ 程度必要になるケースは発見した。

ランダムケースにおける Mo's Algorithm

参考: https://nyaannyaan.github.io/library/misc/mo.hpp.html

ランダムケースでは $\displaystyle \sqrt{\frac{2}{3}} N \sqrt{Q} \approx 0.817 N \sqrt{Q}$ まで落ちる。

*1:正確には対角線付近で中央に戻れないケースがあるのだが、三角不等式を使えば厳密になる。

*2:最悪ケースが最適という意味

2023-04-07

Disjoint Sparse Table に乗るのはやはりモノイドかもしれない。

データ構造

昔の記事で Disjoint Sparse Table には半群が乗るという思想を言ったのですが、使う上ではモノイドにして空の区間に対応した方が嬉しいし、そもそも実装を変えると自然に長さ $0, 1$ の区間に対応できることに気付きました。お騒がせして申し訳ありません。 ACL 風の実装を用意しました。

#pragma GCC target("lzcnt")

#include <algorithm>
#include <cassert>
#include <vector>

namespace noshi91 {

template <class S, S (*op)(S, S), S (*e)()> class disjoint_sparse_table {
  std::vector<std::vector<S>> t;

  int size() const { return t[0].size() - 2; }

public:
  disjoint_sparse_table(const std::vector<S> &v) : t() {
    const int n = v.size() + 2;
    const int h = 32 - __builtin_clz(n - 1);
    t.assign(h, std::vector<S>(n, e()));
    for (int k = 1; k < h; k++) {
      auto &s = t[k];
      const int w = 1 << k;
      for (int i = w; i < n; i += w * 2) {
        for (int j = i - 1; j > i - w; j--)
          s[j - 1] = op(v[j - 1], s[j]);
        const int m = std::min(i + w - 1, n - 1);
        for (int j = i; j < m; j++)
          s[j + 1] = op(s[j], v[j - 1]);
      }
    }
  }

  S get(int p) const {
    assert(0 <= p && p < size());
    return prod(p, p + 1);
  }
  
  S prod(int l, int r) const {
    assert(0 <= l && l <= r && r <= size());
    r++;
    const auto &s = t[31 - __builtin_clz(l ^ r)];
    return op(s[l], s[r]);
  }
};

} // namespace noshi91

t[0] には全て単位元が入っているのがギャグっぽいですが、意味的には自然でクエリの場合分けも消えるし、 $\mathrm{O}(N \log(N) )$ 掛かる初期化に $\mathrm{O}(N)$ の無駄な処理が入っていても良いだろうということで残しています。

2023-04-05

(雑) 転置原理について考えたこと

アルゴリズム

転置原理の競プロでの使い方について考えたことを雑に並べた。普段なら Twitter に書いているような内容だが、長かったので。

転置原理

非常に雑に言うと、以下のような定理である。

$A$ を $m \times n$ 行列とする。「任意の $n$ 次元ベクトル $v$ を入力とし、 $A v$ を計算する」ことができるアルゴリズムがあるなら、同じ時間計算量で「任意の $m$ 次元ベクトル $u$ を入力とし、 $A ^ {\top} u$ を計算する」ことができるアルゴリズムがある。アルゴリズムを具体的に構成することも出来る。

ただし、アルゴリズム内で使える操作に制限があったり、同じ時間計算量と言っても $\mathrm{O}(n + m)$ くらいの違いはあったりする。丁寧な説明は https://qiita.com/ryuhe1/items/c18ddbb834eed724a42b この記事などを読むと良い。

競プロにおける使われ方

計算したい $m$ 次元ベクトル $r$ が、 $m \times n$ 行列 $A$ と $n$ 次元ベクトル $\hat{v}$ を用いて $r = A \hat{v}$ と表せるとする。このとき、 $u$ を入力として $A ^ {\top} u$ を計算するアルゴリズムが発見できれば、転置原理から $v$ を入力として $A v$ を計算するアルゴリズムが存在し、 $\hat{v}$ を入力すれば $A \hat{v} = r$ が計算できる。実は、 $A v$ の計算は難しいが $A ^ {\top} u$ の計算は簡単であるというような例がいくつも存在するので、この議論は有用である。

考えたこと

$n, A, \hat{v}$ をどのように取るかというのは一意ではないので、どう取ると良いのか？という疑問が生まれる。要件は $A ^ {\top} u$ が高速に計算できるようなアルゴリズムを思いつけることである。そこで、 $n = n ^ * , A = A ^ * , \hat{v} = \hat{v} ^ *$ がそのような要件を満たすと仮定する。すると、実は $n = 1, A = r, \hat{v} = 1$ もまた要件を満たすように思われる ( $r$ を $m \times 1$ 行列、 $1$ を $1$ 次元ベクトルと見做している)。 $(A ^ * ) ^ {\top} u$ が高速に計算できるのだから、 $r ^ {\top} u = (A ^ * \hat{v} ^ * ) ^ {\top} u = (\hat{v} ^ * ) ^ {\top} \left ( (A ^ * ) ^ {\top} u \right )$ も高速に計算できることになるからである。結局、競プロにおける転置原理の利用は以下のように言い換えても良さそうに思えてくる。

計算したいベクトルを $r$ とする。 $u$ を入力として $r ^ {\top} u$ を高速に計算できるなら、 $r$ は高速に計算できる。

では、この特殊化された転置原理だけがあれば良いかというと、それも違うかもしれない。まず、 $r ^ {\top} u$ を高速に計算する時、 $r$ を直接求めて内積を取ることはできない。 $r$ を求めること自体が目的だったからである。転置原理の適用条件の都合上、 $r ^ {\top}$ を掛ける操作は何らかの線形変換の繰り返しによるものとなる。すると $A _ 1 A _ 2 \cdots A _ k u$ と計算しているのだが、計算結果がスカラーになるから $A _ 1$ は行ベクトルである。 $A _ 1 = (\hat{v} ^ * ) ^ {\top}, A _ 2 \cdots A _ k = (A ^ * ) ^ {\top}$ とおけば、これは $r = A ^ * \hat{v} ^ *$ と表示していることに他ならない。よって、結局は特殊化されていない転置原理に戻ってきてしまう。

多点評価とその転置を例にして試してみる。 $f(x) = \sum _ {i = 0} ^ {N - 1} c _ i x ^ i$ を $x = a _ 0, a _ 1, \dots, a _ {M - 1}$ で評価することを考える。これに特殊化された転置原理を適用してみると、以下のような問題を考えることになる。

$b _ 0, b _ 1, \dots, b _ {M - 1}$ に対し、 $\sum _ {j = 0} ^ {M - 1} b _ j f(a _ j)$ を求めよ。

この問題の (多点評価を直接使わない) 解法は以下のようになる。

各 $0 \leq i \lt N$ に対して $\sum _ {j = 0} ^ {M - 1} b _ j a _ j ^ i$ を計算する。これは $\sum _ {i = 0} ^ {N - 1} \sum _ {j = 0} ^ {M - 1} b _ j a _ j ^ i y ^ i = \sum _ {j = 0} ^ {M - 1} \frac{b _ j}{1 - a _j y}$ であるから、分数式の和の計算をして各係数を見ればよい。最後に、それらに $c _ i$ を掛けて足し合わせると答えを得る。

正直、これを思いつくのは難しい気がする。一方で、これは多点評価を $A _ {j , i} = a _ j ^ i , \hat{v} _ i = c _ i$ と定義される行列とベクトルの積で表現して、特殊化されていない転置原理を適用していると理解できる。私が個人的に解いてきた転置原理を利用する問題は、多くはこのパターンだったと思う。つまり、

$r$ を求めたい答えとして、 $r ^ {\top} u$ を計算しようとすると、結局 $r = A \hat{v}$ という表現を経由することになる。そのような $A, \hat{v}$ は様々なものが考えられるが、明らかに自然な表現が $1$ つあり、それが $r ^ {\top} u$ の計算にも役立つ。

しかし Bostan-Mori 法を転置した問題では、そのような自然な表現が無い *1。結局、転置原理において特殊化されたものとされていないもののどちらを考えるべきかというのはよく分からない。

*1: 表現はできるのだが、問題設定から自然に思いつけるものではないと思う

2023-04-04

消せる priority queue で消し過ぎない方法

データ構造

概要

std::priority_queue (binary heap) を $2$ つ持って、片方には削除待ちの要素を入れることで、実質的に削除ができるようにするテクニックがある。ただし、これは invalid な削除も可能になってしまう。つまり、存在しない要素 $x$ を削除する操作をした後に $x$ を挿入すると、場合によってはこの $x$ が消えてしまうことがある。これを不可能にする方法を考察してみた。

方法 $1$

std::unordered_(multi)set(map) (hashset) あるいはより高速な自作の hashset を使って、要素が存在するかどうか管理し、invalid な削除を弾く。

利点

invalid になり得る削除をしたい場面では、削除が成功したかも同時に必要になることが多い気がする。この場合 pop を呼ばなければ hashset と全く同じ操作になるので、結局 hashset は必要になる。上手く実装された hashset は高速で、binary heap の $\log$ と比較するとボトルネックにはならない気がする。

欠点

その型に対して hash 関数が定義されている必要がある。速度を気にするなら、その hash 関数の計算時間と散らばりにも気を配らなくてはいけない。 std::unordered_set は遅かった気がするので、これを避けるなら自作 hashset が必要になり、面倒。

方法 $2$

挿入した要素と削除待ちの要素に、それぞれの操作が行われた時刻を記録する。挿入より早く削除されていた場合、その削除は無視する。より厳密には、以下のようなアルゴリズムを使う。

クエリ呼び出しの度にインクリメントすることで、時刻を管理する。
$2$ つの heap には、(priority, 時刻) の対を要素として入れる。priority が等しい要素は時刻が早い方が優先されるようにする。
削除クエリの度に、以下の操作を繰り返し行う。
1. $2$ つの heap の top を見る。
2. 削除側の方が priority が高い、または priority が等しいが削除側の方が時刻が早いなら、削除側だけ pop する。
3. 両者の priority が等しく、削除側の方が時刻が遅いなら、両方同時に pop する。
4. 削除側の方が priority が低い、またはどちらかが空になったら終了する。

正当性

「本体の heap と削除側の heap の要素を時刻順に並べてその通りにクエリを処理すると、真の heap の要素が得られる」という不変条件を維持していることを確認せよ。繰り返しが終了したとき、本体の heap の top は真の heap の top と一致している。

利点

簡単に書ける。

欠点

key が $2$ つの要素の対になったので、比較に時間がかかり、遅くなる。計測していないが、std::set を利用するより遅くなっていたら実用性は無になる。 priority が大きくない整数なら、 $\text{priority} \times 10 ^ 9 - \text{時刻}$ などを key にすれば比較は高速になるかもしれない。

2023-04-02

Universal Cup. Stage 10: Zhejiang. A Atcoder Problem

アルゴリズム

公式解説と違う方法で解いたのだが、その時に使った式変形が面白かったので紹介。

いくらかの計算をすると、次の問題に帰着される。

$W$ 個の非負整数組 $(a _ i, b _ i, c _ i)$ が与えられる。これらは全て $a _ i + b _ i = M$ を満たす。

$\displaystyle \sum _ {i = 1} ^ {W} \frac{c _ i}{(1 - x) ^ {a _ i} (1 + x) ^ {b _ i}}$ の先頭 $N$ 項を $\bmod 998244353$ で計算せよ。

$W \leq 60$

$M \leq 10 ^ {18}$

$N \leq 10 ^ 5$

追記

もっと簡単な方法が紹介されていた。 $\displaystyle F(x) := \frac{c _ i}{(1 - x) ^ {a _ i} (1 + x) ^ {b _ i}}$ とすると、 $F'(x) = \left ( - \frac{a _ i}{1 - x} + \frac{b _ i}{1 + x} \right ) F(x)$ である。分母を払うと $F(x)$ の係数の間に漸化式があることが分かるので、それに沿って計算すれば $O(N)$ である (疎な微分方程式の解)。これを $W$ 回行って足し合わせればよい。

これに気付かなかったの恥ずかしい...

追記終わり

$\displaystyle \sum _ {i = 1} ^ {W} \frac{c _ i}{(1 - x) ^ {a _ i} (1 + x) ^ {b _ i}} = \frac{1}{(1 + x) ^ M} \sum _ {i = 1} ^ {W} c _ i \left ( \frac{1 + x}{1 - x} \right ) ^ {a _ i}$ であるから、以下の問題が解ければよい。

多項式 $f$ は高々 $W$ 個の非零な係数を持つ。 $\displaystyle f \left ( \frac{1 + x}{1 - x} \right )$ の先頭 $N$ 項を求めよ。

まず $f(1 + 2t)$ の先頭 $N$ 項を計算し、次に $\displaystyle t = \frac{x}{1 - x}$ を代入することで計算する。 $f(1 + 2t)$ の計算を先頭 $N$ 項で打ち切ることは、 $\displaystyle \frac{x}{1 - x}$ の定数項が $0$ であることから正当化される。 $f(1 + 2t)$ は二項定理を用いて $\mathrm{O}(NW)$ で計算できるから、残るのは以下のような問題である。

$N$ 次の多項式 $g$ が与えられる。 $\displaystyle g \left ( \frac{x}{1 - x} \right )$ の先頭 $N$ 項を計算せよ。

これは以下のような手順で計算できる。

$\displaystyle \mathrm{rev}(g)(t) = t ^ n g \left ( t ^ {-1} \right )$ を計算する。単に多項式の係数を左右反転するだけでよい。
$t = x - 1$ を代入し、 $\displaystyle (x - 1) ^ n g \left ( \frac{1}{x - 1} \right )$ を得る。(taylor shift)
これの係数を再び反転させ、 $\displaystyle x ^ n \left ( x ^ {-1} - 1 \right ) ^ n g \left ( \frac{1}{ x ^ {-1} - 1 } \right ) = (1 - x) ^ n g \left ( \frac{x}{1 - x} \right )$ を得る。
$(1 - x) ^ n$ で割る。

時間計算量は $\mathrm{O}(NW + N \log(N) )$ である。

後半部分はこの記事と同じ計算をしている。 [多項式・形式的べき級数] 高速に計算できるものたち | maspyのHP 指数部分の和が一定というと使いどころが分かりづらいが、一般に $1$ 次の有理式の代入が $\mathrm{O}(N \log(N) )$ でできると言い換えると見た目は良いかもしれない。