定数倍が最適な Mo's Algorithm

概要

端の移動回数が $N \sqrt{Q} + \mathrm{O}(N)$ 以下の Mo's Algorithm を思いついたので紹介する。

通常の Mo's Algorithm

Mo's Algorithm の問題設定は以下のように言い換えられる。

$0 \leq x \leq y \leq N$ を満たす格子点 $(x, y)$ が $Q$ 個与えられる。 $(0, 0)$ から始めて全ての点を通る経路を構成せよ。経路の長さはマンハッタン距離で測られ、短いほど良い。

スタートが $(0, 0)$ だけではなく任意の $x$ に対する $(x, x)$ であるとか、色々と実用に即したバリエーションは考えられるが、基本的に $\mathrm{O}(N)$ の変化しかないと思う。

通常の Mo's Algorithm は以下のように経路を構成する。

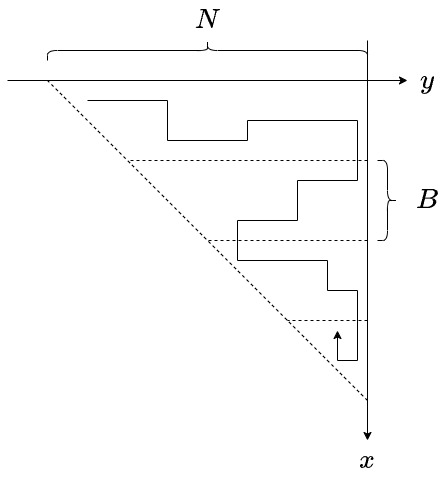
つまり、 $x$ を幅 $B$ 毎に分け、同じ分類の点を $y$ の順に廻る。また、 $y$ の昇降は交互に変化させる。このとき経路長は $\displaystyle \frac{N ^ 2}{2 B} + QB + \mathrm{O}(N)$ 以下となり、 $\displaystyle B = \frac{N}{\sqrt{2Q} }$ とすれば $\sqrt{2} N \sqrt{Q} + \mathrm{O}(N)$ 以下となる。

改善された Mo's Algorithm

$x$ を幅 $B$ で分けた領域を帯と呼ぶことにする。 Mo's Algorithm の最悪ケースは、点が帯の両端に分布している場合である。しかしこの場合、隣り合う帯の端にある点をまとめて通ってしまえばむしろ普通より短くなることが分かる。この発想で、全ての帯を $B / 2$ だけずらした Mo's Algorithm を実行し、元のものとのうち短い方の経路を選ぶというアルゴリズムを考える。

このアルゴリズムの価値は、 $x$ 座標の変化量を $QB$ より精密に評価することで明らかになる。 $l \leq x \lt l + B$ の帯について、 $\displaystyle x = l + B / 2$ を帯の中央と呼ぶことにする。経路を「中央を通って次に訪れたい点と $y$ 座標を揃えたのち、 $x$ 座標を揃え、再び中央に戻る」ものとして解析しても問題ない *1。すると、各点 $(x _ i, y _ i)$ の $x$ 座標に関する経路長への寄与は、属する帯の中央を $x = c$ として $2 \lvert x _ i - c \rvert$ と評価できる。 $\lvert x _ i - c \rvert$ は最悪で $B / 2$ になり得るが、 $2$ 通りの経路におけるそれを合計すると、常に $B / 2$ になることが分かる (！)。よって $2$ 通りの経路の長さの和は $\displaystyle \frac{N ^ 2}{B} + QB + \mathrm{O}(N)$ であり、 $\displaystyle B = \frac{N}{\sqrt{Q}}$ とすれば $2 N \sqrt{Q} + \mathrm{O}(N)$ で抑えられる。このうち短い方は $N \sqrt{Q} + \mathrm{O}(N)$ 以下である。

最適性

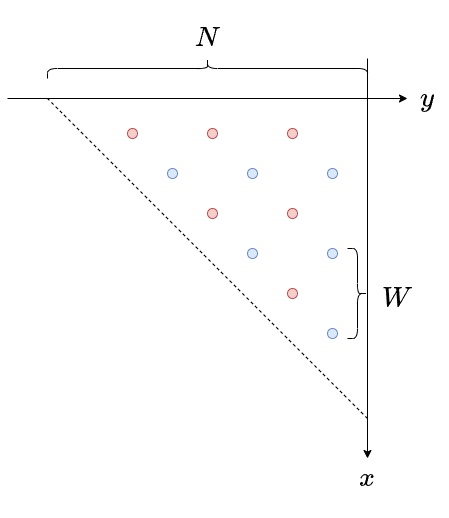
このように点を配置する。赤い点は $1$ 辺に $\sqrt{Q}$ 個配置しており合計で $Q / 2$ 個、青い点と併せて $Q$ 個となる。どの $2$ 点も $W = N / \sqrt{Q}$ のマンハッタン距離があることが分かるから、どのような経路も $Q W = N \sqrt{Q}$ の長さが必要となる。実際には $\sqrt{Q}$ が整数とは限らないこと、格子点にしか点を置けないこと、を考えると $N \sqrt{Q} + \mathrm{O}(N + Q)$ の下限を得る。よって、前述したアルゴリズムは $\mathrm{O}(N + Q)$ の差を除いて最適である *2。

Rollback Mo

参考: https://snuke.hatenablog.com/entry/2016/07/01/000000

同様の考え方を使うと、Rollback Mo も $N \sqrt{Q} + \mathrm{O}(N)$ (Rollback も含めるとこの $2$ 倍) になる。ただしこちらは最適なのか分からない。必ず $\displaystyle \sqrt{\frac{2}{3}} N \sqrt{Q}$ 程度必要になるケースは発見した。