Range Mode Query 空間 Θ(n) 構築 Θ(n√n) クエリ Θ(√n)

概要

Range Mode Query - data-structures

これをもう少しだけ詳しめに解説します。 面白いので好きなアルゴリズムです。

アルゴリズム

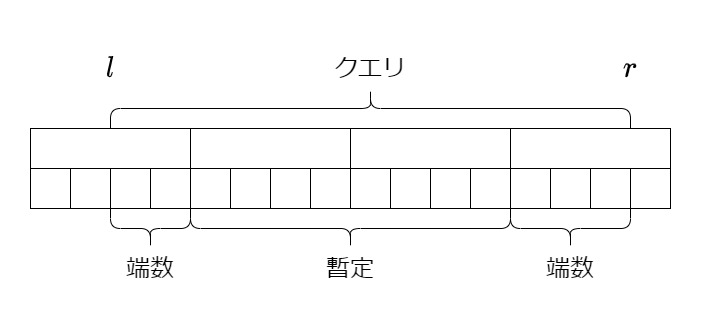
まずは平方分割して、ブロックの境界を端点とする区間 ( 個ある) の全てについて最頻値とその頻度を計算します。 他にも前計算するものがありますが、説明が難しいのでクエリの処理方法を追いながらやっていきます。

区間 の最頻値を計算したいとします。 まずは前計算したものを使って、暫定的な最頻値と頻度 ( ) を取得します。 この暫定解が更新されるとすれば、それはブロックからはみ出た左右の端数の部分に含まれるいずれかの値によるものになります。 従って、端数の部分の全要素について、その要素が に出現する回数が を超えるか判定して、適切に更新する、というアルゴリズムがまず思い浮かびます。

クエリを にしたいので、それぞれの要素について で頻度を取得したくなりますが、 の空間計算量でこれは絶望的です。

そこで見る方向を変えて、「左側の端数部分に含まれる各要素 について、その 個後ろの の位置が より手前にあるか」という判定を考えます。 この判定自体は、全ての数についてその数だけ抜き出した index の列を持っておけば空間計算量 、時間計算量 で可能です。 これを用いた「 より手前にあったら が更新されるということなので、 を 1 増やして繰り返す」というアルゴリズムは、 の時間計算量になります。 なぜなら、ステップを 1 つ進めるたびに「 では更新されなくなったので、次の数に移る」「 が 1 増える」のいずれかが発生し、 は最初の暫定解から しか増え得ないからです。 右側の端数部分に含まれる数については逆に、 個手前の の index が より後ろにあるかを判定すれば全く同様です。