重心分解で 1 点更新区間取得

概要

木上の等高線集約クエリ - suisen のブログこの記事で未解決になっていた変種 $1, 1'$ を解決する。

$M$ を可換モノイドとし、 $N$ 頂点の木 $T$ の各頂点には $M$ の元が書き込まれているとする。

$v \in V(T)$ に書かれている値を $x \in M$ に書き換える。
$v \in V(T)$ から距離 $a$ 以上 $b$ 未満の頂点に書かれた値の総和を出力する。

以上のクエリを前計算 $\Theta(N \log(N))$ 、 $1$ クエリ $\Theta( (\log(N) ) ^ 2)$ の時間計算量で処理できる。ただし $M$ の演算は $\mathrm{O}(1)$ で可能とする。

また、同様の手法によって区間作用 $1$ 点取得も処理できる。 JOI 2021/2022 春合宿 day3-2 がこの問題だが、時間計算量的に通るかどうかはよく分からない。

距離が辺の重み付きで定義される場合も前計算が $\Theta(N (\log(N) ) ^ 2)$ かかるものの同様に処理できる。

アルゴリズム

概要で述べた記事の内容を概ね理解していることを前提とする。

$T$ から重心を取り除いたときに分かれる部分木たちを $L$ とする。従来の手法で問題となっていたのは、重心の次数が $\lvert L \rvert$ になってしまい、ここの処理に時間がかかるという点である。そこで、 $L$ を一度に重心に付ける $\lvert L \rvert$ 分木ではなく、 $V(T)$ と対応しないノードを間に挟み二分木を作る。

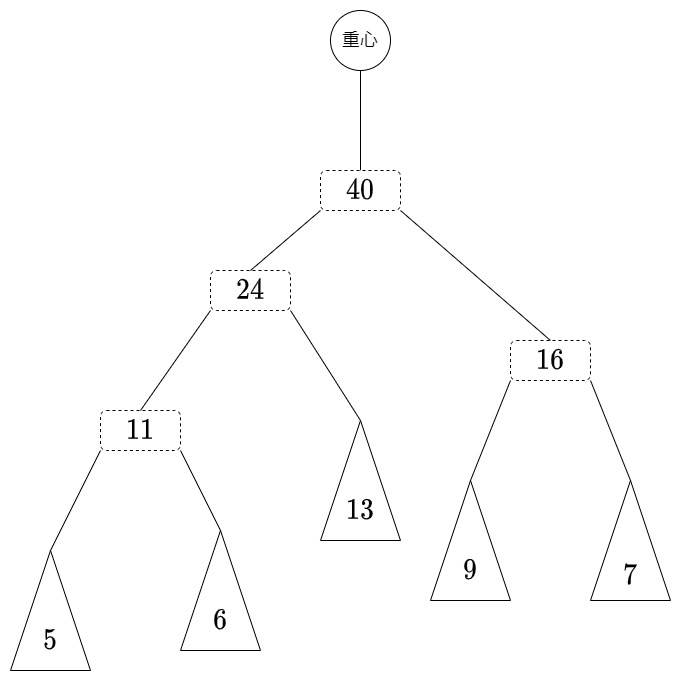
f:id:noshi91:20220327041409j:plain

上図において実線の三角形は $L$ の元であり、点線の長方形は $V(T)$ に対応しない新たに追加されたノードである。書き込まれた数は後述するアルゴリズムにおける重みである。

新たに追加されたノードについても、その子孫の頂点たちを深さ順に並べて Segment Tree で管理する。また、 $L$ の元については従来の重心分解同様、再帰的に重心を取り除き木構造を作成し、得られた根付き木を $U$ とする。この状態で更新クエリを処理することを考えると、 $U$ において $v \in V(T)$ から根に至るのパスの長さが $\mathrm{O}(\log(N) )$ になっているかどうかが問題となる。 $L$ の元の重みをその部分木の頂点数として $L$ を葉とする Huffman coding の木を作ることで、それが達成される。具体的には以下のアルゴリズムを実行する。

$Q := L$ とする。
の間、以下を繰り返す。
- $Q$ から重みが最小及び $2$ 番目に小さい元を取り出し、それらを子とするノードを作成する。作成されたノードの重みを子の重みの和と定義し、 $Q$ に追加する。

$U$ において $v \in V(T)$ から根に至るパス $P$ の長さを考える。 $x \in V(U)$ の重み $w(x)$ を、 $U$ において $x$ の子孫である $T$ の頂点の個数と定義する。 $P$ において $v$ の次に現れる $T$ の頂点を $x$ とすると、 $v$ - $x$ パスの長さは $c + c \log(w(x) / w(v) ) \cdots \bigstar$ 以下である。これは $v$ の親を $2$ つ辿ると $w$ が $2$ 倍以上になるためであり、Huffman coding の木を作るアルゴリズムから証明できる。 $P$ において $T$ の頂点が現れる回数は重心分解自体の性質により $\mathrm{O}(\log(N) )$ であり、 $\bigstar$ の第 $1$ 項の和は $\mathrm{O}(\log(N) )$ となる。 $\bigstar$ の第 $2$ 項の和は telescoping sum の形であるから $\mathrm{O}(\log(N) )$ となる。