省メモリな区間 add 区間 min

概要

長さ の数列 に対する区間 add と区間 min を時間計算量 で処理する、空間計算量 のデータ構造を説明する。 ただし、一連の操作における の最大値を としたとき、 の範囲の数を管理するために必要な空間計算量を としている。

例: 長さ の数列に の加算クエリが 回ほど行われる状況では、 bit 整数 個のメモリで処理できる。

構造

簡略化のため、 が の冪の場合をまず考える。 Segment Tree と同様に、配列を用いて二分木の構造を作る。 まず、各ノードに対して対応する区間内の最小値を考える (この値は実際には保持しない)。 続いて、各ノードに対して左子 右子を計算し、これを保持する。 葉には子が無いので、データは保持しない。 すると下図のような構造となる。

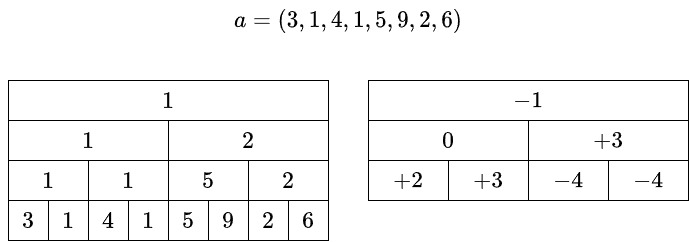
この右側のデータに加えて全体の最小値も持つことで、Segment Tree に対するものと似たようにクエリの処理が可能となる。 例えば区間 add では、データを適切に更新しつつ、着目しているノードの区間の最小値の増分を返すような関数を設計すると良い。 区間 に を加算するクエリは以下のようになる

1. 着目しているノードの区間が に完全に含まれているなら、 を返す。
2. 着目しているノードの区間が と交差しないなら、 を返す。
3. 左子と右子に対して再帰的に加算クエリを行う。それぞれの返り値から着目しているノードの値を更新し、返り値を計算する。

が の冪でない場合も、空間計算量が の Segment Tree と同様に完全二分木でない二分木構造を作ればよい。 ノードの個数は になるため、全体の最小値の管理と併せて 個の整数を管理することになる。