概要
- 長さ
の広義単調増加な整数列
が与えられたとき、
を満たす広義単調増加な整数列
の個数
を
の時間計算量で計算できる。
- 上記の設定に加えて
の下限も与えられる場合も、同じ計算量で計算できる。
(,),?からなる長さの文字列が与えられたとき、
?を(または)に置き換えて得られる文字列であって valid な括弧列になるものの個数を
の時間計算量で計算できる。
- 見た目の異なる
つのアルゴリズムがある。どちらが高速かは未検証。
単調増加列の数え上げ
列の数え上げを経路の数え上げで言い換える。
例えば の場合、以下の図において赤い点から右か上に進んで青い点に至る経路の個数と等しい。

経路の数え上げなので、 掛けた単純な DP でひとまず答えは出ることが分かる。
さらに分割統治法の都合上、左下から右上への経路の数え上げというのを強めて以下の問題を考える。
上図のような階段状の盤面が与えられ、赤い点にはそれぞれ何らかの値が書き込まれている。 ここから経路数え上げの DP を行ったとき、最終的にそれぞれの青い点に書き込まれる値を求めよ。
これを分割統治法で解く。 まず、下辺の中心から上に直進し、盤面に突き当たったら右に直進すると、下図のように長方形領域が切り取られる。(盤面を簡略化して三角形風に描いている)

そして、左下の領域において DP を計算する (赤矢印)。 これは再帰的な呼び出しで実現できる。 次に、中央の長方形部分において DP を計算する (青矢印)。 これは寄与が二項係数で表されるので、丁寧に式変形をすると畳み込みになることが分かる。 最後に、右上の領域において再帰的に DP を計算する (緑矢印)。
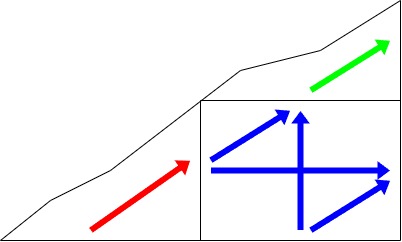
時間計算量は である。
下限もついている場合

上図のように盤面を分割すると、分割されたそれぞれの領域を前述したアルゴリズムで順々に計算していくことができる。
時間計算量は再び となる。
括弧列の数え上げ
(,),?からなる長さの文字列が与えられる。
?を(または)に置き換えて得られる文字列であって valid な括弧列になるものの個数を数えよ。
文字列に含まれる ? の個数を とする。
長さ
の数列
を考え、
を、
個目の
? を ( に置き換えるなら ,
) に置き換えるなら と定義する。
すると、
から成る数列
が valid な括弧列に対応する条件は「
という条件が各
についてあり、
については等式で成り立っている」といった形のものになる。
これを図で表してみると、以下のような図における経路の数え上げとなる。

×印で禁止されている場所以外にも、赤点から青点への経路として通ることが不可能な場所がある。 そのような無駄な部分を削除すると、下図のようになる。
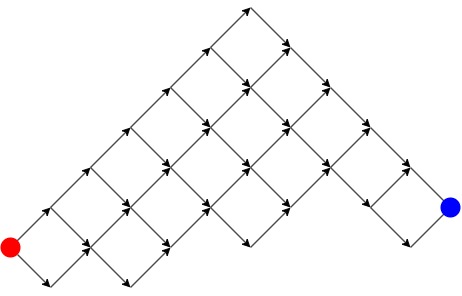
これは回転すると単調増加列の数え上げと同じ形である。
亜種のアルゴリズム
本節は、https://codeforces.com/contest/1770/problem/G この問題の公式解説を私が再解釈して記述したものである。

単調列の数え上げも、括弧列の数え上げも、上図のような経路の数え上げに帰着できるのであった。 括弧列の節で言及したとおり、上の方に到達不能な部分があるが、無限に広がっていると思う方が都合がよいのでそのままにしている。 この図では右下か右上かに進むことを繰り返す経路が得られるが、これが右と右上になるように盤面を線形変換すると下図のようになる。

ここで、分割統治のために一般化した問題を考える。
上図の赤辺部分に値が書き込まれている。右か右上に進めるとして経路数え上げの DP をしたとき、青辺部分に書き込まれる値を求めよ。
赤辺を青辺の下端の高さで上下に分け、それぞれについて青辺への寄与を計算する。 赤辺上部の青辺への寄与は単に二項係数で表されるので、畳み込みで計算できる (緑矢印)。 赤辺下部の青辺への寄与は分割統治法により計算する (水色矢印)。

このアルゴリズムの優秀な部分は、 が
冪になるように調整すれば、畳み込みの部分で使いまわしが効くようになることである。
記事中前半で紹介したアルゴリズムでは、
を
冪にしても畳み込みの部分では中途半端な値が出てきてしまうので使いまわしができない場所がある。
しかし上手くやればできるかもしれないし、全体を通してどちらが高速なのかは未検証。
また、このアルゴリズムを上限と下限のある単調列の数え上げに適用できるかも不明である。

