top tree 概要
概要
top tree の記事が出ていたので、あまり触れられていない部分を補足していくモチベーションで書きました。
segment tree を知らないと読んでもあまり面白くないと思います。
link cut tree を知っていれば分かりやすいです。
その手のデータ構造の問題のネタバレをいくらか含んでいます。
概念
| 列 | 木 |
|---|---|
| 区間 | cluster |
| 区間の端 | boundary vertex |
| モノイド | ?(演算が複数あるよく分からないやつ) |
| 赤黒木, AVL木 等 | topology tree, link cut tree*1 等 |
セグ木や平衡二分木などは共通の「区間がマージ可能なとき、それを木構造で表現する」という枠組みを持っていました。
top tree はこれを列から木に拡張するとイメージすることができます。
区間と対応する概念として、部分木よりもやや強い条件のある cluster を考えます。
cluster とは木の部分木 *2 であって、外部との接点が 2 つ以下であるものを言います。
この外部との接点を boundary vertex と呼びます。
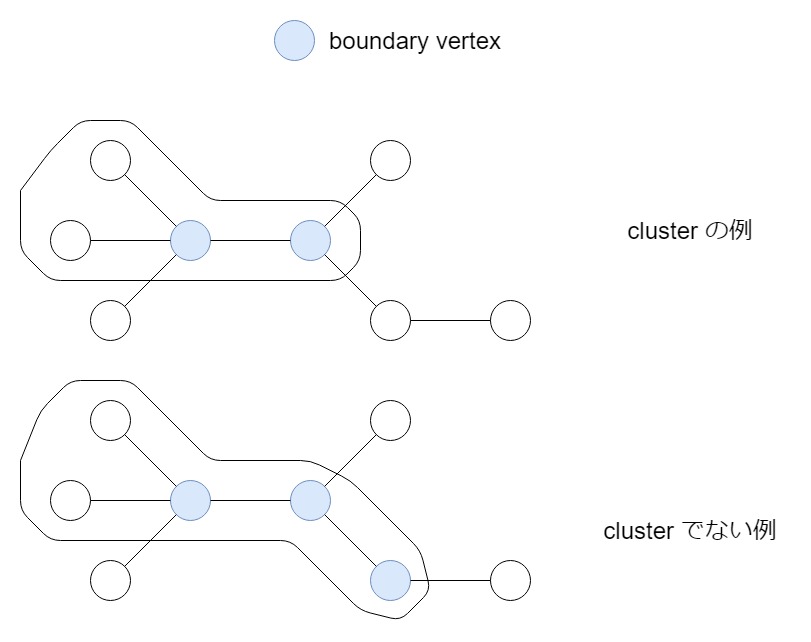
この 2 つ以下の条件が列に対する区間の綺麗な一般化になっている訳です (区間の端点は 2 つ以下)。
これによって cluster に対し「接点 1, 2 からの最大距離、内部の最大距離、接点 1,2 間の距離」を持つことで直径が計算できるようになります。
これは Do Use Segment Tree で使うモノイドととてもよく似た構造です。
よって「cluster がマージ可能なとき、それを木構造で表現する」ことが出来れば良いです。
これはかなり汎用的な枠組みなので、平衡二分木に色々あるのと同様、link cut tree に限らず topology tree と呼ばれる動的木などにも乗せることが出来るようです (文献参照)。
競プロ的には link cut tree (のままだと乗らないので改造した奴) に乗せるのが実用的で、top tree と言うとこれを指すような風潮を感じます。
操作
- link, cut
いつもの動的木 - expose
指定した頂点を接点に持つ cluster を根に持ってくる
取得クエリや更新クエリは expose 後に根を直接操作する - search
欲しい辺を発見する関数
木を 2 つに分けた cluster が与えられるので、欲しい辺がどちらの cluster に属しているか指定する関数を引数に与える
例えば重心なら、重いほうの cluster を指定すればいい
構造
link cut tree をベースにしたものを説明します。 top tree ではパスだけでなく部分木も適切に和を取る必要があります。 link cut tree ではある頂点から出る light edge は親方向に辺を持つだけで親側からは見えませんでしたが、この light edge たちを splay tree でまとめあげ、親側からもたどれるようにします。
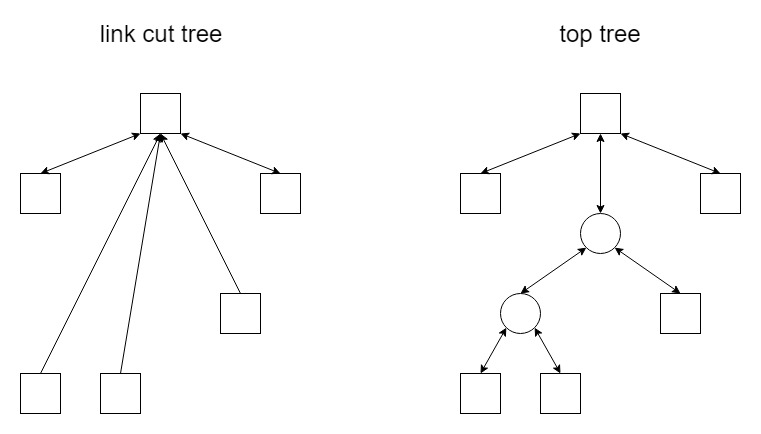
全てのリンクが双方向になっている等の点に注目してください。
この状態でも適切に splay をすることで expose が可能であり、計算量も Ο(logN) に抑えられる、というのが大雑把な解説となります。
external boundary vertex を用いた頂点の更新の定式化などは論文を読むと分かります。
文献
Stephen Alstrup, Jacob Holm, Kristian de Lichtenberg and Mikkel Thorup. Maintaining Information in Fully-Dynamic Trees with Top Trees
[cs/0310065] Maintaining Information in Fully-Dynamic Trees with Top Trees
cluster 等の諸概念を導入し、動的木に乗せたら色々できるということを示している。
後半も色々書いてあるのだが、競プロで使えるかよく分からなかったのと辛くなったので読んでいない。
どういうことが出来るかや具体例、各種操作の定式化などはこれを読むとよい。
Robert E. Tarjan and Renato F. Werneck. Self-Adjusting Top Trees
http://citeseerx.ist.psu.edu/viewdoc/download?doi=10.1.1.87.9754&rep=rep1&type=pdf
前述した構造が link cut tree のような自己組織化する動的木に乗ること、辺の順序も管理できることを示している。
具体例が多く link cut tree を知っていれば多分分かりやすい。
競プロで実用的なのは恐らくこの実装である。
雑記
実装しようとするとコーナーケースが多くてめっちゃ心が折れる、強い意志で頑張って欲しい。
早すぎる抽象化と高速化は首を絞めがちなので注意して欲しい。
追記: 書きました。 Top Tree の構造の変種 - noshi91のメモ